Tyger! Tyger! burning bright
In the forests of the night,
What immortal hand or eye
Could frame thy fearful symmetry?
—“The Tyger” by William Blake

“Does the world embody beautiful ideas?” This is the question that kickstarts Nobel laureate and Templeton Prize winner Frank Wilczek’s magisterial exploration of the concept of beauty as a guide star for the science of physics. Wilczek’s 2015 book A Beautiful Question answers his query on page one eschewing dramatic suspense and leaving us in no doubt that the next 300 pages will detail just how much beauty nature embodies and how much of this exquisiteness physicists have been able to capture in their equations. 

For Wilczek, nature is nothing less than a work of art which calls on us to assess if “it is a successful work of art?” – a task he takes as tantamount to asking, 

The theme of beauty in physics has a long and storied history tracing a chain of ideas articulated by many of the field’s most famous practitioners. Galileo, Newton, and especially Johannes Kepler (the father of modern astrophysics) all believed that God had created the universe according to elegant mathematical laws which a rightly-tuned mind could discern. For these giants of the scientific revolution, the mathematical beauty of the universe constituted a “divine harmony” – the so called “music of the spheres” – a kind of celestial composition expressing itself in terms of numbers and equations. And like great human-made music, the “music of the cosmos,” as written by the Creator, was ipso facto taken to be something that should stir the hearts of men.

Jump forward to the mid-19th century when physics entered its truly modern era with the introduction of the concept of fields – as in electric, magnetic, and gravitational fields – and along with them, the development of intense new mathematical tools to describe these ineffable “states of space.” Here, Wilczek tells us, science entered into uncharted terrain where intuition and inspiration would have led the way, advancing far beyond what experimental evidence could, then, reveal.  

By what “inspired guesswork” was this new physics driven, Wilzcek wonders? Particularly the enigmatic equations formulated by James Clerk Maxwell to express the interactions between electric and magnetic fields? Logical consistence was a necessary principle, but hardly sufficient, he remarks. Rather, Wilczek says, “It was beauty and symmetry that guided Maxwell and his followers,” – a cadre in which he doesn’t hesitate to include “all of modern physicists.”

Maxwell – Wilczek’s “favorite physicist” – is the Isaac Newton of the post-mechanical age of science and the pioneering genius behind the modern modality of mathematical abstraction in physics, a tradition to which Wilczek himself has contributed so much. 

***

Today, it is taken for granted that physicists must traffic in mathematical arcana – the more abstract the better, it sometimes seems – but in the late 19th century this move was contested by many physicists who viewed the mathematization of their field as a betrayal of its raison d’etre. It was, after all, called “physics” not mathics. No less a figure than Lord Kelvin, the science rockstar of his age (a kind of Victorian Stephen Hawking), railed against Maxwellian formalism and insisted that behind physicists’ theories of the world there should always be a concrete physical model with a mechanistic explanation for any given phenomena.

Kelvin lost this battle and formalism won out. Ever since, equations have served as a reservoir of insight into how the world works, with the internal qualities of abstract formulae increasingly leading to insights about nature’s operation.

Take perhaps the most famous example: Dirac’s prediction of antimatter. When Dirac wrote out a relativistic equation for the electron in 1928, he found the equation had two solutions, the second of which suggested the existence of an opposite particle to the electron, one with similar properties but a positive charge. Though he initially resisted taking this possibility seriously – Oppenheimer was the first to do so – Dirac came to see that the math implied all particles have a mirror-image twin with opposite electric charge. Today we call this stuff “antimatter.” Dirac eventually proposed there was an entire antimatter mirror universe, a kind of doppelganger to the world we experience with antiparticles and antiatoms. All this inspired by the solutions of an equation. 

In 1932 Carl Anderson found evidence for the existence of Dirac’s anti-electrons, which came to be called “positrons.” Formalism had proven itself not just as a theoretical nicety but as a wellspring of real-world discovery. When asked once what he thought about his equation, Dirac replied, “I found it beautiful.” 

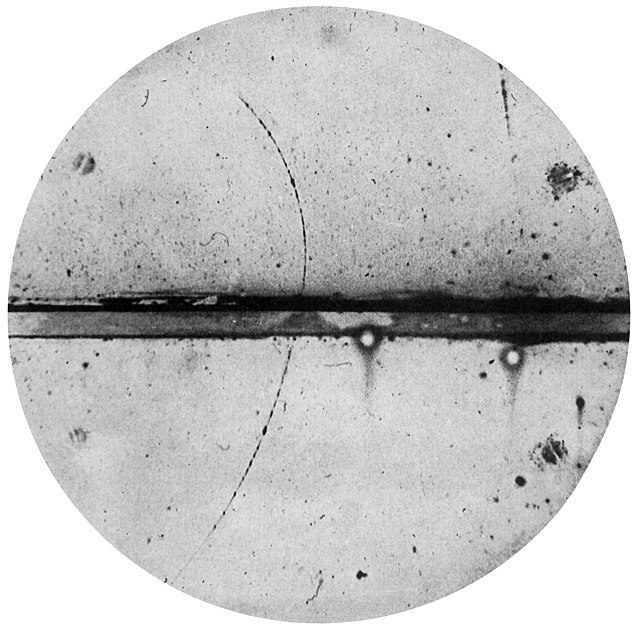
The first-ever positron identified, photographed by Carl Anderson.

Einstein too declared his general theory of relativity so elegant it had to be right. Queried on how he’d react if it turned out to be wrong, he responded bluntly, “I’d feel sorry for the dear Lord.” How could such formal beauty not be right?

Wilczek, whose work on mathematical physics has made him one of the most celebrated scientists today – winner of the Nobel Prize, the Dirac Prize, the Templeton Prize among others – sums up his modus operandi thus: “I often follow Plato’s strategy, proposing objects of mathematical beauty as models for Nature.” Like Maxwell, Dirac, and Einstein, Wilczek has discovered extraordinary real-world phenomena in the abstract refinement of equations.

But what do physicists mean when they talk about beauty? What characteristics fall under this banner for them? Given how so many of them have stressed its guiding role, it’s no trivial matter to wonder what exactly the term signifies to a working physicist. After all, different cultures across the globe offer very diverse notions about what “beauty” might be. Indigenous Aboriginal artifacts from my homeland Australia, for example, have little in common with Western notions of aesthetics, and until recently were barely recognized as embodying any conception of elegance. Likewise, visiting the astonishing collection of Congolese artifacts in the Natural History Museum in Berlin, one is struck by the sheer alien-ness of objects whose organizing paradigms and internal arrangements seem almost impossible to grasp from within the perspective of European stylings. 

***

So, what is beauty to a physicist?

Perhaps no-one has answered more concisely than Herman Weyl, who helped to pioneer the mathematical relationship between general relativity and electromagnetism and who formulated the first gauge theory of elementary forces and particles. “Beauty,” Weyl says, “is bound up with symmetry.”

Weyl expresses his admiration for symmetry in his short pithy 1952 treatise on the subject in which he explores how concepts of symmetry play out play out in the history of art, in the  structures of organisms, in the formations of crystals and snowflakes, and which, he says, serve as a continuing inspiration to both mathematicians and physicists. Symmetry, Weyl notes, is “an idea by which man through the ages has tried to comprehend and create order, beauty and perfection.” Wilczek agrees, also identifying symmetry as perhaps the single-most important concept guiding modern physics. 

One can see Dirac’s antimatter as a direct consequence of taking mathematical symmetry seriously. Here, an equation suggested both positive and negative solutions – a not uncommon situation in math itself, where we often have a number (like 5) and its negative (-5) as valid solutions. Oppenheimer, and later Dirac, dared to say the negative solution also represented a real-world particle. Which initially seemed absurd. How could reality manifest a “negative” particle? 

Some historians have claimed that antimatter represents the first time an equation led to the discovery of a wholly new physical phenomenon; and certainly, it’s an important case in the history of science. But we can argue that Maxwell did something similar half a century before. As Wilczek shows so well in his book, Maxwell was also stirred by notions of symmetry when formulating his electromagnetic equations; and his commitment to mathematical symmetry in his physics allowed him to discern an equivalence between electric and magnetic fields which led him to the astonishing conclusion that light is waves of electromagnetism travelling through space.

This remains one of the most extraordinary, and unexpected, discoveries in all of physics – in all of science really – born out of nothing more, and nothing less, than a willingness to take conceptual symmetry as a guide to the real world.

Reading Wilczek and Weyl’s paeans to symmetry one can’t help but think of William Blake’s much-quoted poem:

Tyger! Tyger! burning bright
In the forests of the night,
What immortal hand or eye
Could frame thy fearful symmetry?

Blake was much opposed to what he saw as the reductionism of science in the face of the nature’s glories. Along with Keats, who wrote that Newtonian science would “unweave the rainbow” and destroy its charm, Blake saw science as an opposing force to imagination. Yet in his poetic defense of nature he singles out the very quality in which modern physicists have found so much inspiration – and so much practical achievement.

***

Why is symmetry so appealing to physicists? Why such an emphasis on this quality? Weyl again cuts to the core by noting that symmetries encode various kinds of “invariance” – qualities of things which endure through some kinds of transformation. He and Wilczek each give the example of the circle – which can be rotated by any number of degrees yet which remains the same. Compare this to a square, which only remains the same when rotated by 90˚, 180˚, 270˚ or 360˚. Or a hexagon, which has 6 rotational symmetry positions. 

Long ago, Plato extolled the circle as the most perfect geometric form (along with the its 3D cousin, the sphere) and insisted the heavenly bodies must travel around the Earth in perfect circular orbits, thus building symmetry into the foundations of Western science. Weyl and Wilczek both declare themselves unabashed Platonists searching for aspects of nature which stay the same under more complex kinds of transformations. Wilczek calls this “change without change,” alluding to qualities which endure – the underlying mathematical symmetries – in the face of changing physical appearances.

The fruitfulness of this idea can be seen over and over again in the physics of the past century, with one of the loveliest examples due to Wilczek himself – so-called “time crystals.” 

We are all familiar with ordinary crystals, like salt, or the wondrous collections of minerals in natural history museums. These are structures whose atoms take on regular or periodic arrangements in space. In the early 2010’s Wilczek wondered if there might be an equivalent kind of structure whose periodicities played out in time; he named them “time crystals.” This again seemed quixotic, but in 2016 experimentalists made such a form and have since continued to create others. By positing a symmetry between structures in space and in time Wilczek predicted a phenomenon that may one day be used in quantum computer memory.

***

Symmetry, however, is a very particular type of beauty, so we may well ask if there are limits to its validity as a principle in physics. The first person to intuit such limits was one of the founders of modern physics, Johannes Kepler. Few people in history have been so besotted on symmetry as Kepler, who spent a decade trying to create a model of planetary motion based on the symmetries of the Platonic solids, which all map onto the sphere. Kepler’s Platonic-solid model failed to fit with astronomical data, and from out of the ashes of this disaster he was forced to abandon the 2,000-year-long Western obsession with circles. By allowing himself to deviate from “pure” symmetry, Kepler discovered that the orbits of the planets aren’t circles, but elipses – a much less regular form. 

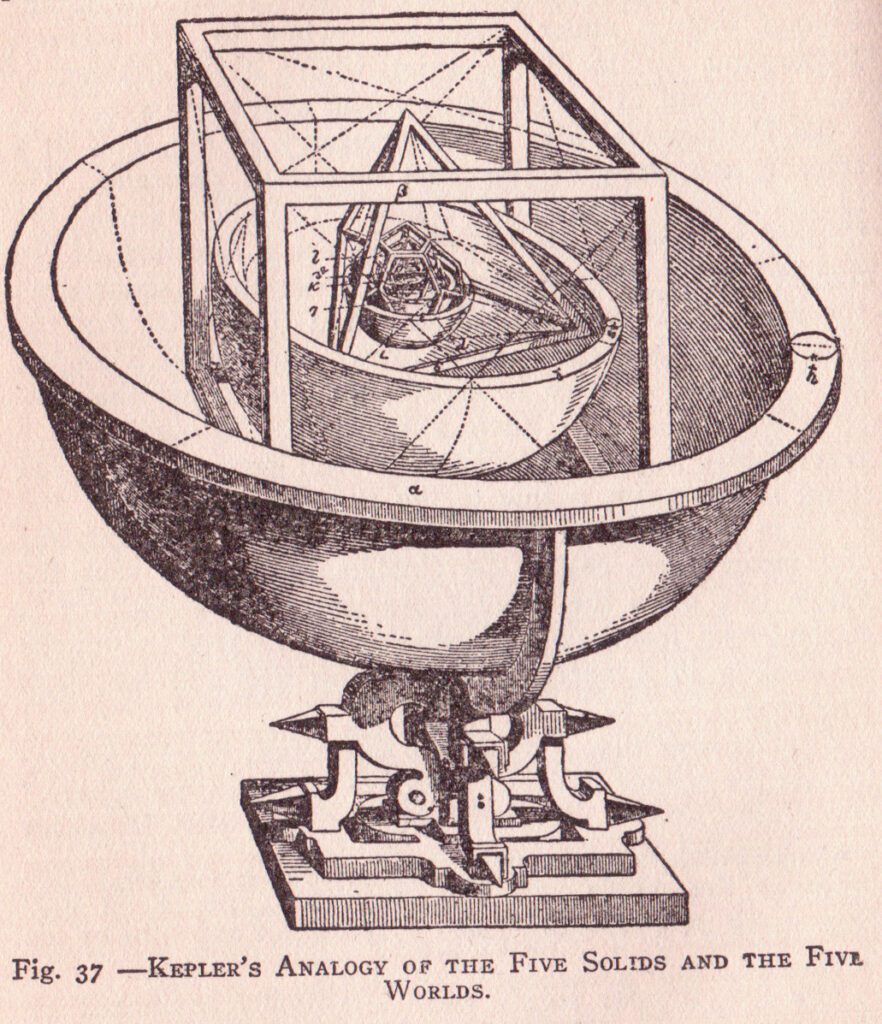
Kepler’s Analogy of the Five Solids and the Five Worlds.

This is the moment when astrophysics was born for Kepler’s laws of planetary motion served as a scaffold on which Newton built his understanding of gravity.

Historian of science Fernand Hallyn, in his magnificent book The Poetic Structure of the World, analyses Kepler’s astronomy and compares it to that of his predecessor Copernicus. Though Copernicus is often mythologized as the first modern, Hallyn suggests he is anything but, because Copernicus was still wedded to the Platonist circle-dogma and could not conceive of planetary motions having any physical cause. Kepler’s transition from circles to elipses wasn’t just a mathematical move, because he believed they must reflect a genuine physical force – what Newton later identified as gravity.

Yet on top of this reasoning, Hallyn has a fascinating aesthetic point to make about the shift from Copernican to Keplerian cosmology. Copernicus, who remained fixated on circles, was also, Hallyn says, a man of the high Renaissance, whose picture of the cosmos fitted with Renaissance artists’ love of geometric symmetry. Copernicus life (1473-1543) overlapped with Leonardo da Vinci’s (1452-1519) and Raphael’s (1483-1520), both leading practitioners of geometric perspectival techniques. Leonardo hired Paccioli to teach him mathematics and Raphael explored geometry in relation to the cosmos in his great series of frescoes in the Vatican Palace.

The truncated icosahedron, described by Leonardo Da Vinci as Ycocedron Abscisus Vacuus.

Kepler (1571-1630) lived in the Mannerist period and according to Hallyn his elipses also reflect the more relaxed aesthetics of this time – a willingness to be more imaginatively wild in painting and in philosophy, a capacity to let go of Platonist “perfection.”

I think there are lessons here we can carry into our own time. Symmetry may be a virtue, a kind of beauty from certain perspectives – especially if one is looking for what is unchanging in the world – but it cannot be our sole guide. Weyl himself points to its limits when he quotes early on in his book the art historian Dagobert Frey from the latter’s essay “On the Problem of Symmetry in Art.” Frey notes that symmetry “signifies rest and binding, asymmetry motion and loosening, the one order and law the other arbitrariness and accident, the one formal rigidity and constraint, the other life, play and freedom.” 

This fits in with Hallyn’s assessment of Copernicus and Kepler, the former obsessed with “formal rigidity,” the latter more able to see “play and freedom” in the world.

While the beauty of symmetry has been, and still is, serving as a guide to some kinds of natural phenomena – electromagnetism, antimatter, time crystals, and the theory of “supersymmetry” in particle physics, for example – physicists’ obsession with it may also be taken too far.

Sabine Hossenfelder, a German theoretical physicist, has written about the limits not just of symmetry but the whole idea of beauty in physics. For Hossenfelder, adherence to this principle is leading physics today vastly off-track. Writing in Aeon magazine (based in her book Lost in Math: How Beauty Leads Physics Astray), she lists a series of failures from this line of inspiration: the prediction that protons should decay; dark matter “WIMP” particles; extra dimensions of space; and supersymmetry particles. Hossenfelder is blunt in her assessment: 

Physicists must rethink their methods, now – before we start discussing whether the world needs a next larger particle collider or yet another dark matter search.”

I think I stand in the middle ground here, admiring the inspiration of beauty yet agreeing with Hossenfelder that physics needs, in some sense, to lighten up. We can all learn from Kepler – my favorite physicist – “perfection”’ isn’t always the way nature works.